Molti di quelli che avranno provato a capire cos’è e come si calcola R_t probabilmente si saranno fermati ad un certo punto perché l’argomento diventa troppo tecnico.

Anche i fisici dell’INFN, quando hanno cominciato a studiare l’argomento hanno trovato diverse questioni ostiche che hanno meritato giornate di studio della letteratura che non era familiare a chi si occupa per mestiere di nuclei e di particelle elementari e non di virus.

Sul nostro sito abbiamo provato a spiegare alcuni aspetti salienti dei principali algoritmi che sono usati in letteratura. L’Istituto Superiore di Sanità (ISS) propone una dettagliata FAQ (Frequently Asked Questions) per spiegare come viene calcolata la stima ufficiale di R_t, dalla quale dipende il destino della nostra regione, che potrebbe finire, in base a quel risultato, in zona rossa.

In questo post proviamo a spiegare un elemento del calcolo di R_t usato dall’ISS che può essere di difficile comprensione per chi non è esperto di statistica, ma che ha importanti aspetti concettuali, legati ai fondamenti del metodo scientifico. Si tratta dell’approccio bayesiano alla probabilità, e alla stima dei parametri ignoti, quale è R_t.

Leggendo le FAQ dell’ISS fino in fondo, troviamo il cuore del metodo per la stima di R_t:

La stima di R(t) viene effettuata con un metodo statistico consolidato [1], che stima la distribuzione a posteriori tramite un algoritmo Markov Chain Monte Carlo (MCMC) applicato alla seguente funzione di verosimiglianza […]

Il metodo statistico consolidato è riportato nella referenza [1], ossia il seguente articolo:

[1] Cori A, Ferguson NM, Fraser C, Cauchemez S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am J Epidemiol. 2013;178(9):1505-1512. doi:10.1093/aje/kwt133

Il metodo applica la tecnica delle Markov Chain Monte Carlo (MCMC), uno dei metodi numerici più usati per risolvere i problemi noti come inferenza bayesiana. Si tratta di uno dei metodi statistici che permettono di stimare dei parametri, nel nostro caso R_t, a partire da un campione di dati. Nel nostro caso il campione dei dati è il numero di persone infette giorno per giorno. In particolare, l’ISS usa il numero di infetti sintomatici. Noi useremo il numero di persone infette che è riportato quotidianamente dal Dipartimento della Protezione Civile.

E qui viene il cuore del nostro post: in cosa consiste l’inferenza bayesiana, e come differisce da altri metodi statistici utilizzati ampiamente nella letteratura scientifica?

Dobbiamo prendere la questione un po’ da lontano, e spiegare brevemente come viene intesa la probabilità in senso bayesiano.

Esistono due principali definizioni di probabilità utilizzate in statistica e in applicazioni scientifiche:

• probabilità frequentista
• probabilità bayesiana

Con l’approccio frequentista, la probabilità viene definita come la frazione, o equivalentemente la percentuale, di casi in cui si verifica un certo evento. Ad esempio, se lancio tante volte una moneta, il 50% dei casi avrò testa, il 50% invece avrò croce. Si otterrà sempre il 50% solo nel limite in cui riuscissi a lanciare la moneta infinite volte, cosa che nessuno avrebbe il tempo, tanto meno la pazienza, di fare.

Con l’approccio bayesiano, invece, la probabilità misura quanto sia credibile un evento. In altre parole, quanto sarei disposto a scommetterci. Inevitabilmente, questo approccio è soggettivo. Infatti, diverse persone riterranno più o meno credibile un evento in base alle informazioni che hanno a disposizione, e che possono essere diverse da individuo ad individuo. L’approccio bayesiano, tuttavia, non dice che la probabilità può essere definita in maniera arbitraria da ciascun individuo. Prescrive, invece, un metodo matematico rigoroso per modificare in modo razionale il proprio livello di conoscenza della probabilità di un evento in base ai dati di cui si ha conoscenza. In altre parole, si parte da una conoscenza della probabilità a priori per passare ad una probabilità a posteriori che deve essere modificata per tenere conto delle evidenze che ci forniscono i dati.

Tralasciamo qui gli aspetti matematici, ma forniamo alcuni esempi, prima di passare al calcolo di R_t. Chi volesse approfondire, può trovare qui un articolo con diversi riferimenti bibliografici.

Nella due figure che seguono, consideriamo la stima del valore centrale di una insieme di osservazioni.

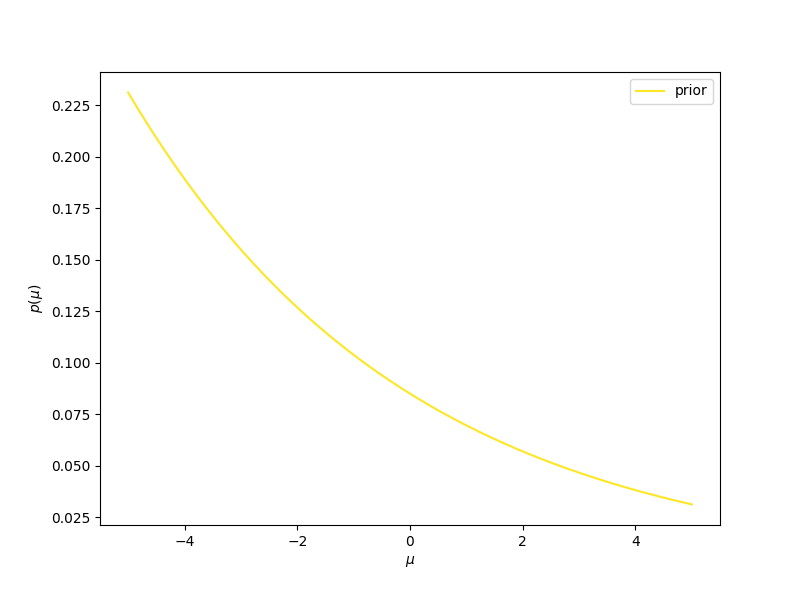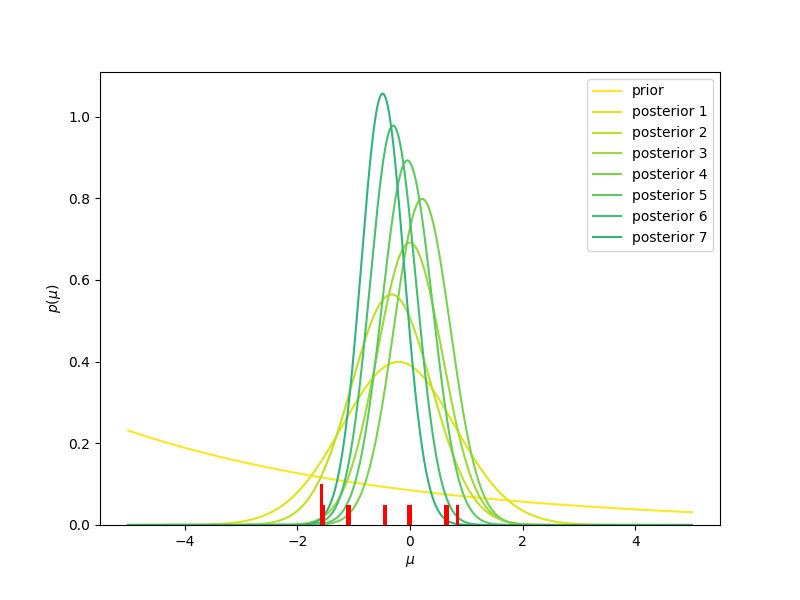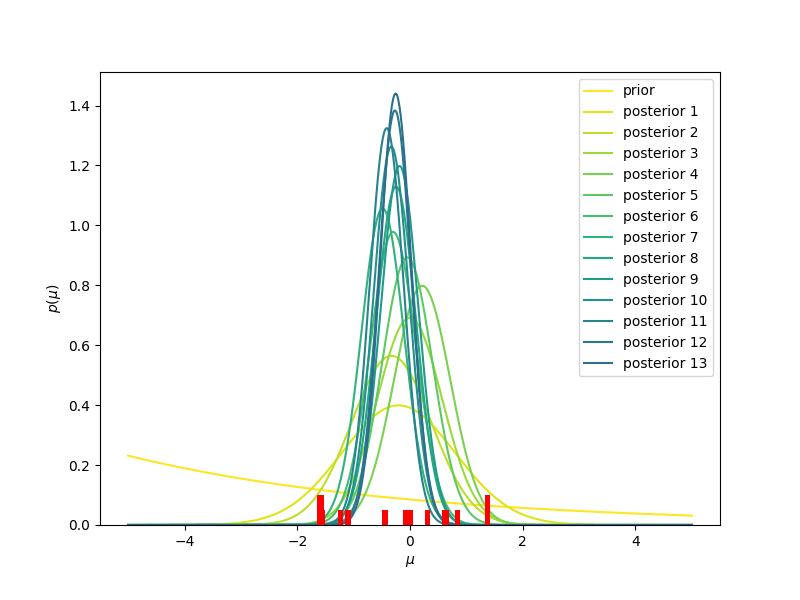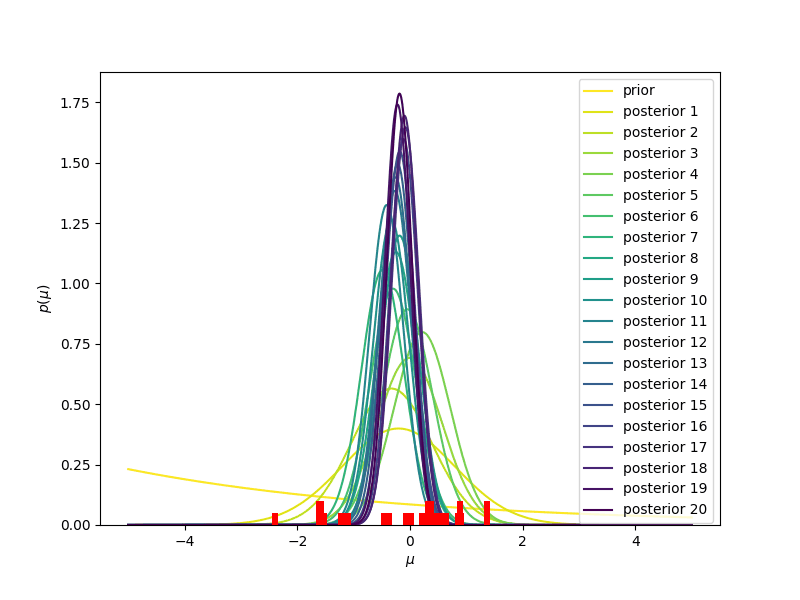
1. Se inizialmente immaginiamo che la nostra probabilità a priori (indicata con prior, nella figura) è la stessa per tutti i valori (la linea gialla, corrispondente ad una distribuzione uniforme), man mano che osserviamo nuovi valori (mostrati in rosso, in basso nella figura) dobbiamo aggiornare la nostra probabilità a priori, che diventerà probabilità a posteriori (posterior 1, 2, …. 20, nella figura). Vediamo che la distribuzione a posteriori diventerà sempre più stretta e centrata intorno al valor medio, che in questo caso è sempre più vicino allo zero, man mano che aggiungiamo informazione. Usare una distribuzione uniforme come modello iniziale della nostra probabilità a priori significa dare un significato quantitativo alla nostra ignoranza iniziale: per noi un valore qualsiasi va bene come un qualunque altro valore. Diremo che la nostra probabilità a priori non è informativa.
   
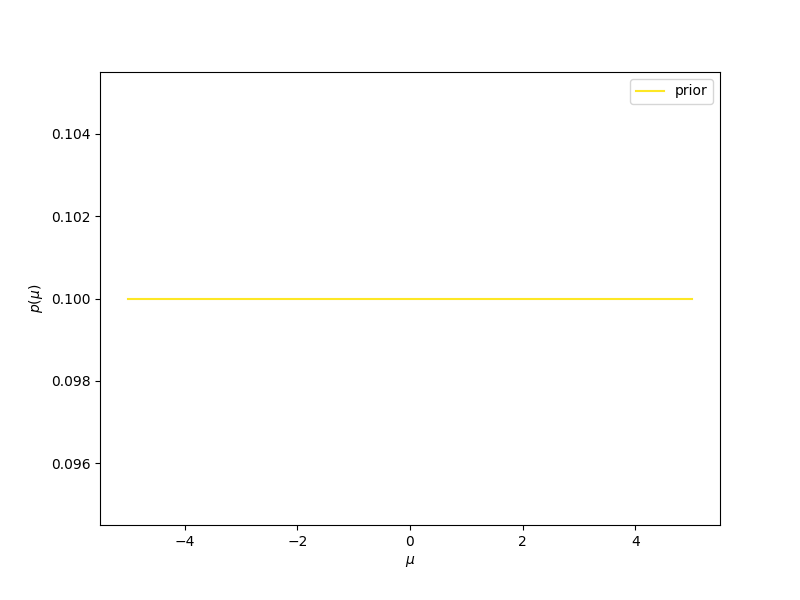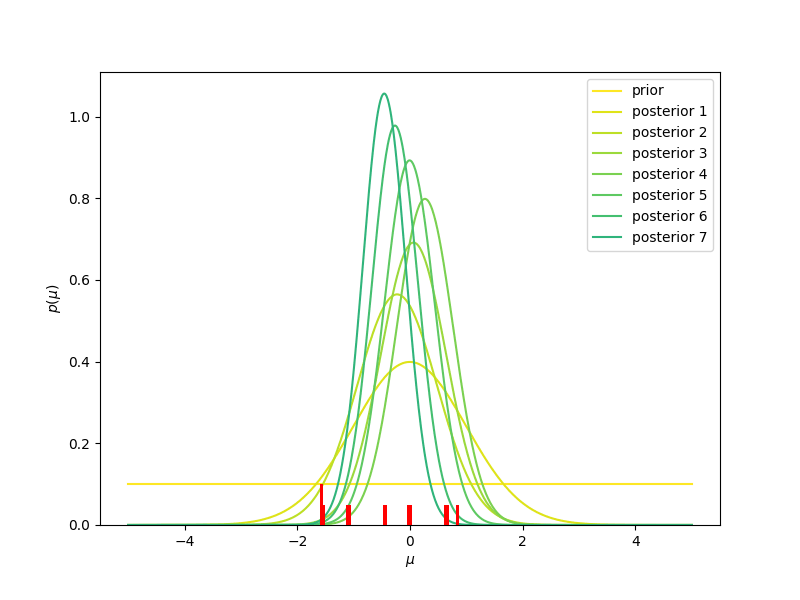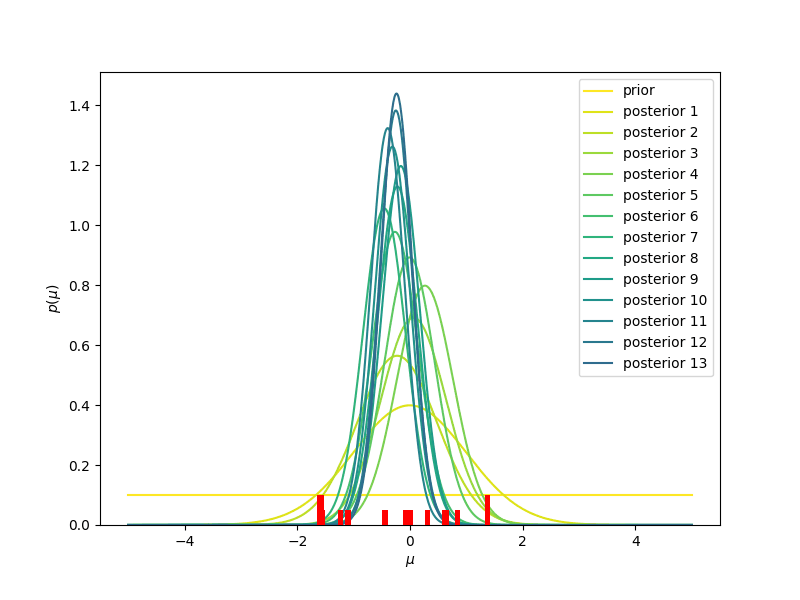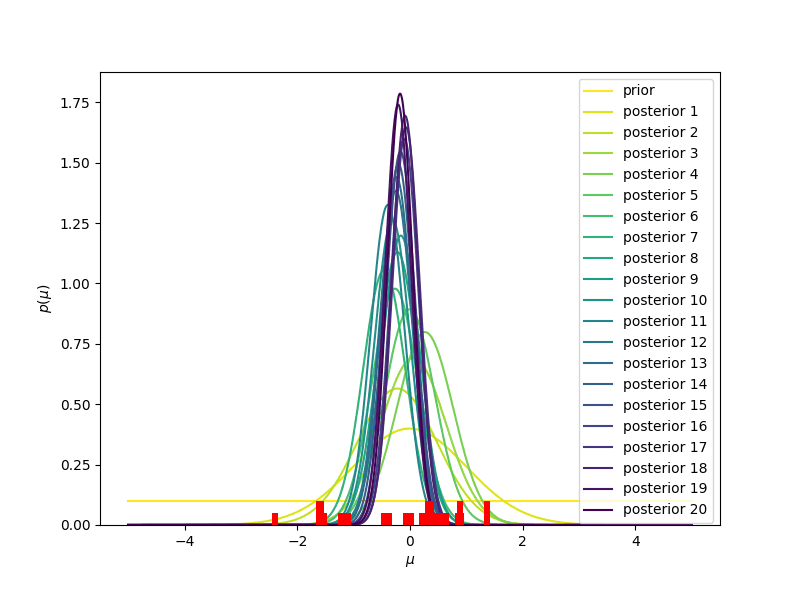
2.   Se invece partissimo da una distribuzione che privilegia i valori negativi (linea gialla nel grafico qui sotto, corrispondente ad una distribuzione esponenziale decrescente), perché abbiamo qualche motivo per credere che i valori negativi siano più probabili, man mano che osserviamo nuovi valori la nostra distribuzione di probabilità a posteriori ancora una volta diventerà più stretta e centrata intorno allo zero. Più informazioni, ossia dati, e possibilmente precisi, vengono considerati, e più la distribuzione di probabilità a posteriori dimenticherà la probabilità a priori, iniziale, per assestarsi verso una distribuzione determinata per la gran parte dai dati, e in misura sempre minore dal nostro a priori.
   

Veniamo ora al calcolo di R_t. L’algoritmo utilizzato dall’ISS, anche utilizzato per altre applicazioni, si chiama EpiEstim ed è implementato nel linguaggio di programmazione R. I dati del numero di persone infette giornaliere vengono utilizzati da un algoritmo che usa l’approccio bayesiano e che, necessariamente, come abbiamo visto, deve assumere una distribuzione di probabilità a priori per il valore di R_t che deve essere determinato.

I parametri che possono essere modificati quando viene eseguito l’algoritmo sono specificati nella documentazione. Non è possibile specificare una qualsiasi distribuzione, ma viene assunta una distribuzione asimmetrica (in modo da non avere mai valori negativi, che per R_t non avrebbero senso) che ha un valore centrale ed una dispersione. Entrambi possono essere specificati dall’utente. Per chi volesse provare a girare l’algoritmo EpiEstim, sono i parametri mean_prior e std_prior. I valori di default dell’algoritmo sono 5 ± 5. Ovvero, assumiamo che il valore che riteniamo più credibile sia R_t= 5, ma riteniamo piuttosto ragionevoli anche valori più piccoli, così come valori che possono arrivare fino a 10.

Quale può essere una scelta ragionevole per la distribuzione a priori? E soprattutto: quanto questa scelta influenza il valore che andremo a stimare?

Per diverse malattie è stato determinato il numero di riproduzione di base che misura quante persone sono infettate da una persona a sua volta infetta in caso non sia applicata alcuna misura preventiva per ridurre l’infezione. Questo valore viene anche detto R₀. Sappiamo ad esempio che R₀ può andare da 0.9 a 2.1 per l’influenza stagionale, tra 1.4 a 2.8 per l’influenza spagnola,  e tra 12 e 18 per il morbillo. Per il coronavirus Sars-Cov-2, responsabile del COVID-19, R₀ è stato stimato tra 2.2 e 5.7. Ci aspettiamo che le misure restrittive riducano R_t a valori inferiori rispetto ad R₀.

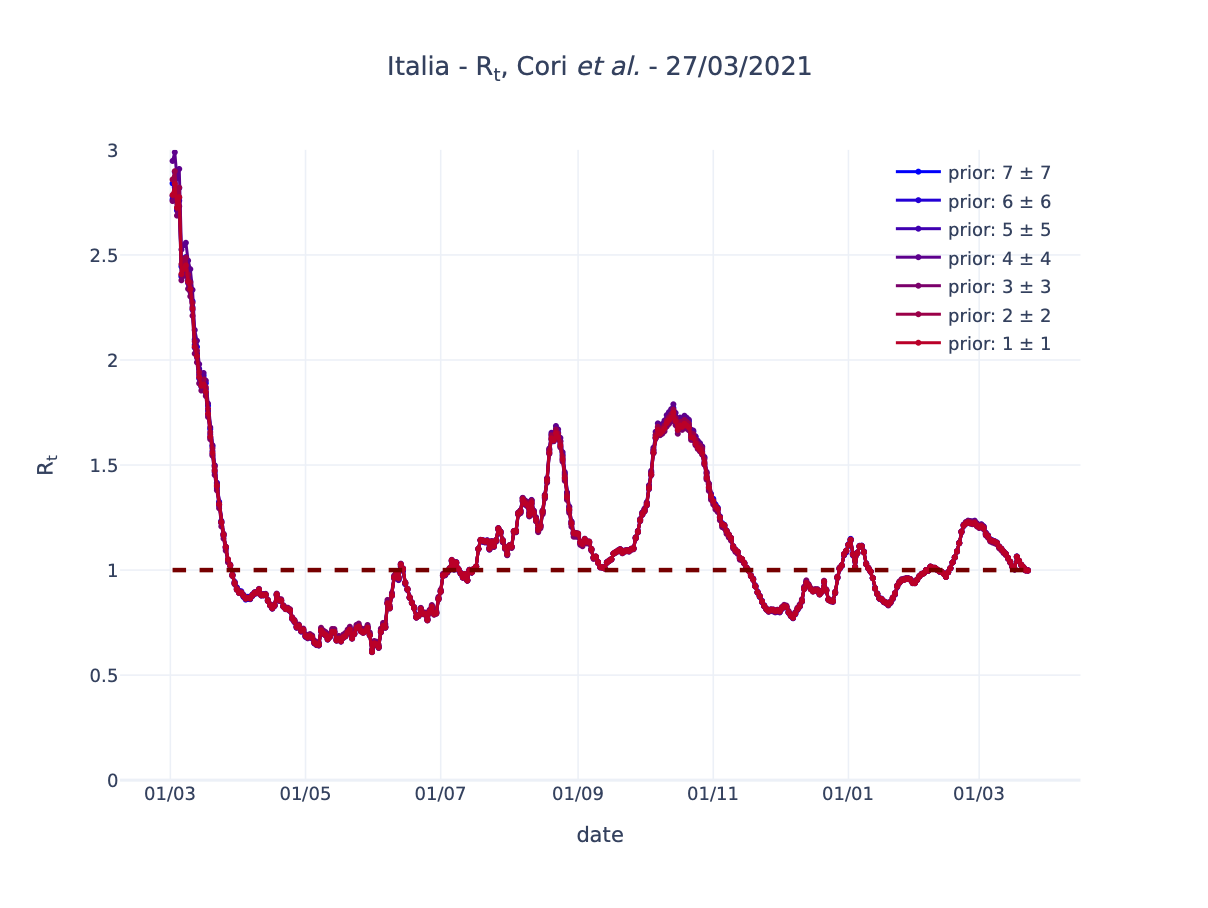
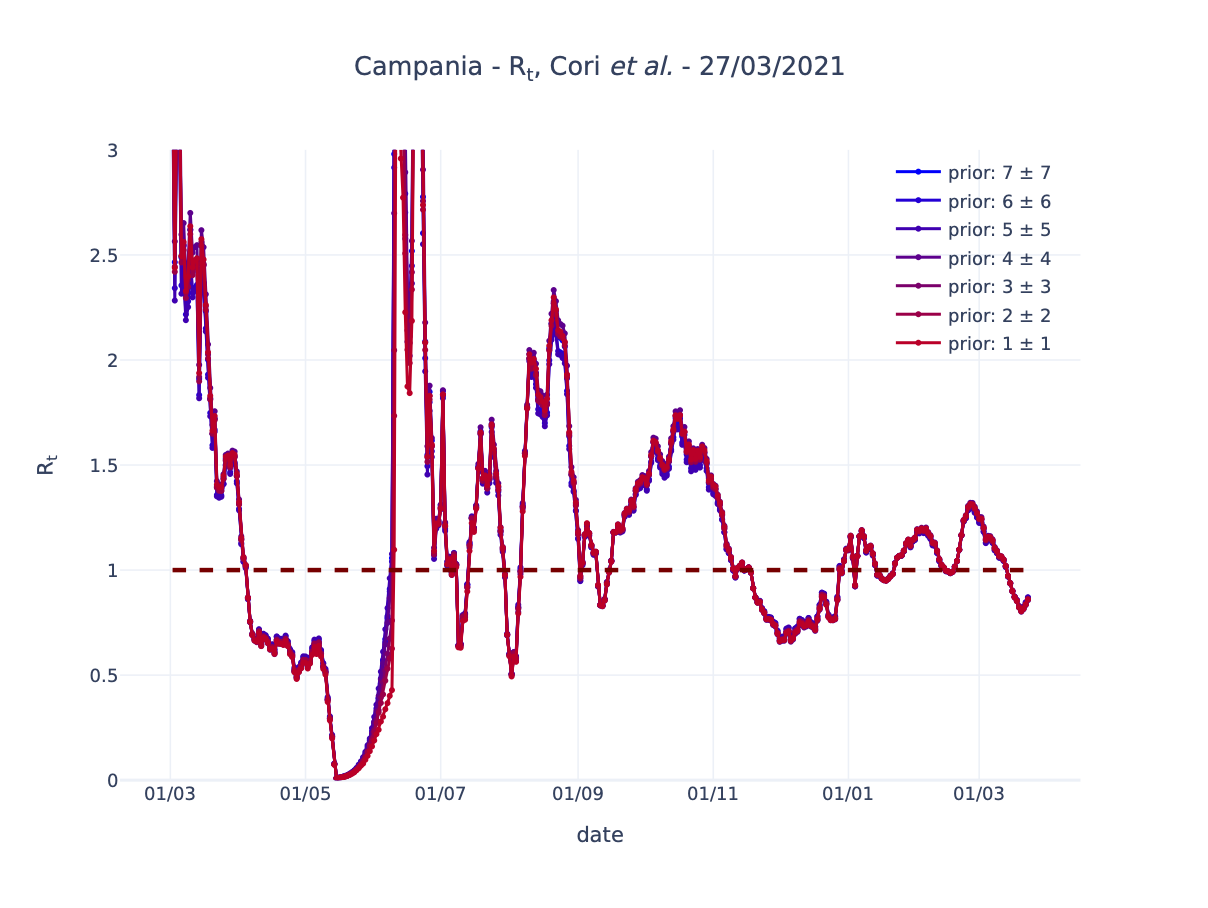
Abbiamo provato a modificare la distribuzione a priori usata dall’algoritmo EpiEstim partendo dai valori 1 ± 1 fino a 7 ± 7 ed abbiamo ripetuto il calcolo per l’Italia e per alcune regioni italiane.

Quello che abbiamo osservato è quanto segue.

• Il passaggio per il valore soglia 1, così come valori vicino ad 1, non sono modificati in maniera rilevante dalla scelta della distribuzione a priori. Questa proprietà generale la abbiamo discussa in un nostro articolo  [arXiv:2012.05194].
• L’Italia soffre meno di Lombardia e Campania della scelta della distribuzione a priori perché è presente un numero maggiore di casi che forniscono una stima più stabile. Questo è vero in particolare per i valori di R_t più alti, dove invece le regioni possono avere una maggiore variabilità in base alla scelta della distribuzione a priori.
• Il Molise, a causa dei pochissimi casi registrati quest’estate, ha in quel periodo una stima di R_t fortemente dipendente dalla scelta della distribuzione a priori.

In conclusione, oltre alle diverse fonti di incertezza da cui e affetta la stima di R_t, la scelta della distribuzione a priori, quando si usa l’algoritmo EpiEstim, in alcuni casi, potrebbe non essere trascurabile.  Il contributo dominante all’incertezza resta comunque la stima del tempo medio di ritardo tra infezione primaria e secondaria, come è discusso in un nostro articolo [arXiv:2012.05194].

Per essere certi di non avere una stima fortemente dipendente dalla scelta della distribuzione a priori, potrebbe essere utile confrontare il risultato ottenuto con diverse scelte possibili e verificare che le differenze non siano importanti.