I dati inerenti ad un qualsiasi fenomeno possono essere rappresentati, tra i tanti modi possibili, anche in un grafico, particolarmente se si vuol fornire un modo rapido per evidenziarne l’andamento. Una tabella numerica potrebbe essere del tutto sufficiente allo scopo (in fondo i dati già possiedono tutta l’informazione che sul fenomeno abbiamo collezionato) ma il nostro modo più rapido di percepire il mondo è tramite la vista, non tramite il ragionamento astratto, basato su numeri.

Ecco perchè il nostro sito presenta un così elevato numero di figure: l’andamento nel tempo di un fenomeno può essere colto dallo sguardo in modo molto più efficiente mediante un grafico che non mediante un’attenta lettura dei singoli valori numerici. Naturalmente le due rappresentazioni contengono lo stesso numero di informazioni, il grafico non ne fornisce di più, ma il nostro occhio sa estrarre significati più rapidamente mediante una sguardo che non mediante un’attenta valutazione dei numeri

Ma come si legge un grafico? Come si estraggono le informazioni utili in esso contenute?

Anzitutto osserviamo che esistono diverse tipologie di grafici: gli andamenti nel tempo, i grafici di correlazione, le rappresentazioni tridimensionali, quelle di tipo geografico e molte, molte altre. Iniziamo il nostro breve excursus nel modo della rappresentazione grafica dei dati dalla categoria più comune, gli andamenti temporali, le cosiddette time-lines.

Un andamento temporale è un grafico che rappresenta la variazione di una certa quantità misurabile al passare del tempo. Sull’asse orizzontale si pone il tempo (espresso nelle unità più utili per il caso specifico, minuti, anni, millenni o quant’altro) e sull’asse verticale, in corrispondenza di un certo istante, si pone il valore assunto dalla quantità (di cui vogliamo rappresentare l’andamento) in quel particolare momento.
Se la quantità non varia nel tempo, otterremo una linea orizzontale, se cresce avremo una linea che tende verso l’alto. Se scende ne avremo una verso il basso e, più in generale, potremo avere una linea che andrà su e giù.

Consideriamo ad esempio i dati forniti sulla situazione del COVID19 dalla Protezione Civile per la giornata dell’11 Febbraio 2012, come evidenziata in questa tabella:

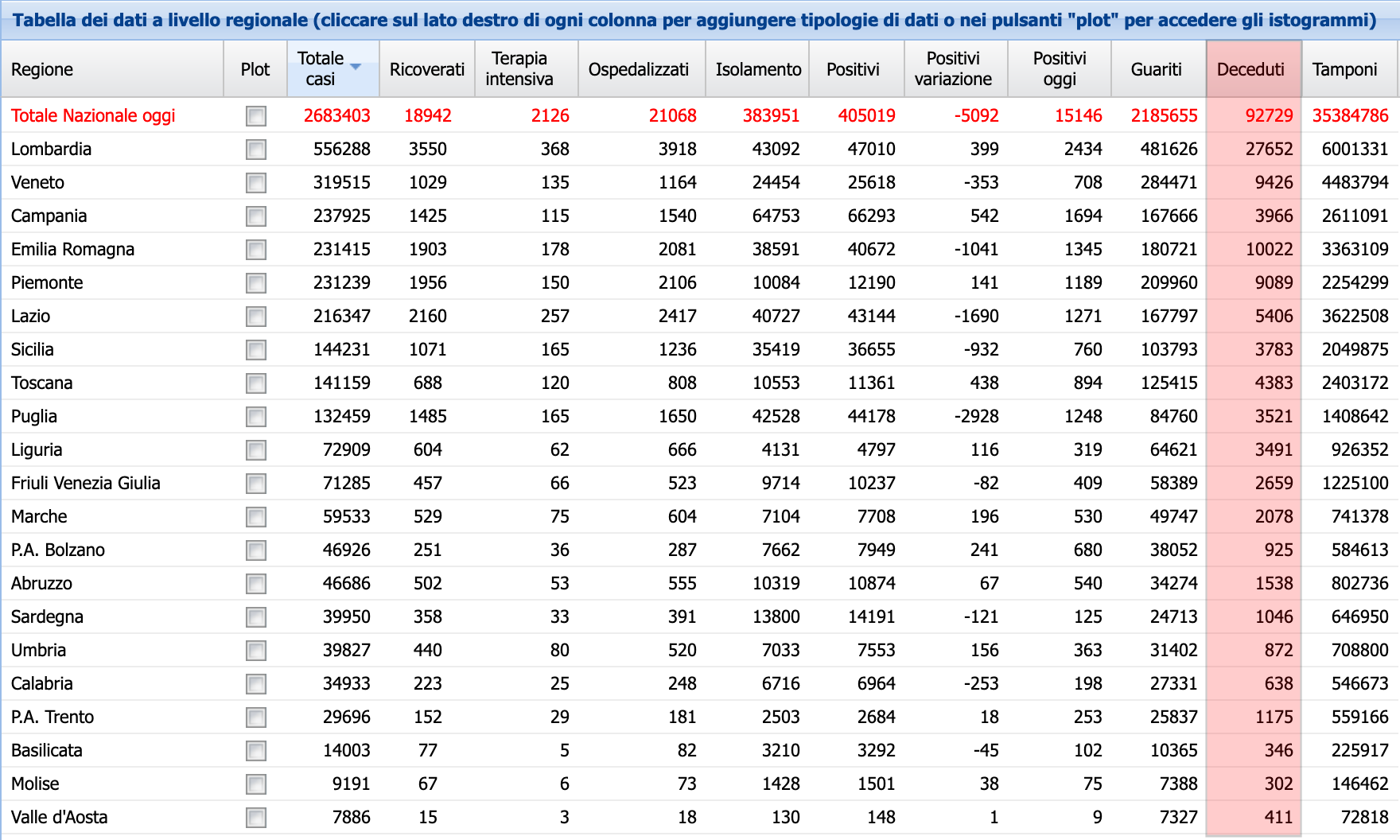Figura 1. Dati forniti quotidianamente dalla Protezione Civile

Si tratta di molti numeri, è difficile trarne delle consclusioni ad occhio, con un solo rapido sguardo. Del tutto impossibile poi capire da questa sola tebella se i casi di persone decedute, ad esempio, stiano aumentando o diminuendo rispetto al giorno precedente (semplicemente perchè questi ulteriori dati non sono contenuti in questa tabella, che si riferisce a un solo giorno). Ma se anche avessimo le tabelle di tutti i giorni precedenti, è chiaro che ci perderemmo in un mare di dati. Possiamo invece fare una cosa più utile, trasformare le tabelle di vari giorni in un unico grafico:

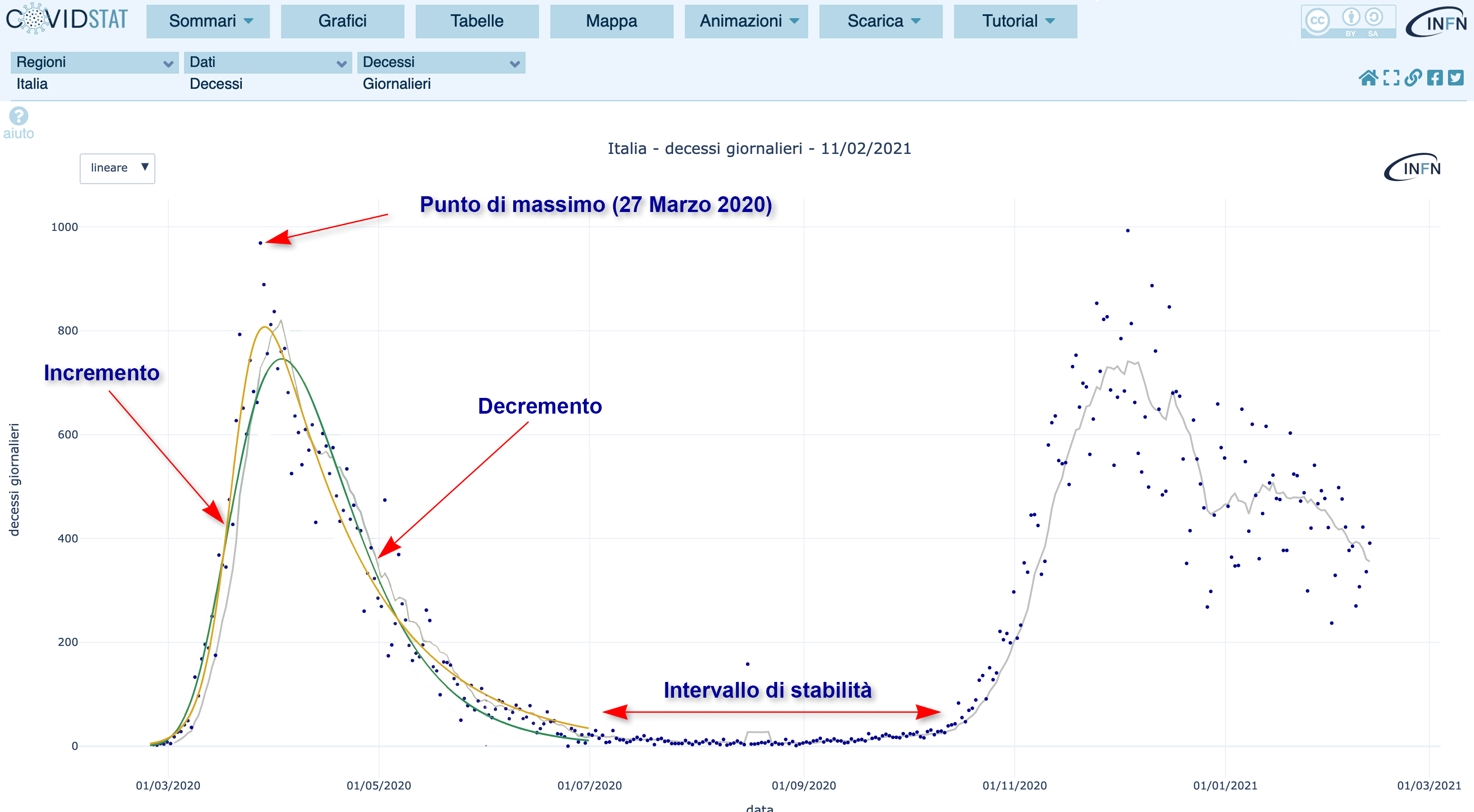Figura 2. Andamento quotidiano dei decessi in Italia a partire da 24 Febbraio 2020

Cosa osserviamo da questo grafico? Anzitutto notiamo che l’asse orizzontale, quello dei tempi, contiene le date a partire da 24 Febbraio 2020 (primo giorno per il quale la Protezione Civile ha iniziato a rilasciare i dati pubblicamente) fino al primo di Marzo del 2021. Sull’asse verticale ci sono invece i valori che indicano il numero di persone decedute. In corrispondenza di ogni singolo giorno tra le due date indicate, viene poi disegnato un pallino blu all’altezza che corrisponde al numero di deceduti in quel particolare giorno. Si ottiene un andamento che sale e scende: il minimo, di zero deceduti al giorno per COVID19, lo si osserva solo prima del 24 Febbraio e per qualche sporadico giorno in estate .

Diventa a questo punto evidente ad occhio l’andamente temporale del numero di deceduti: dopo un primo picco nel Marzo 2020 (fino a un massimo di più di 900 morti in un singolo giorno), si assiste ad una lenta discesa nell’estate, un prima lenta risalita a partire da Giugno seguita da una rapida escalation di valori fino a superare, in Dicembre, i ricoverati di Marzo. Si osserva anche come la decrescita di questa seconda ondata sia più lenta di quella della prima.

Bene, è chiaro a questo punto come un grafico permetta una lettura più agevole che non una tabella di numeri.  Vediamo ora di distinguere due tipi di grafici diversi: essi rappresentano la stessa quantità ma con un diverso andamento temporale. Nella figura precedente abbiamo rappresentato i dati “giornalieri“: ogni singolo punto blu del grafico rappresenta il numero di deceduti di quel giorno particolare. Qui sotto vediamo un grafico (figura 3) , apparentemente diverso dal precedente, ma che reappresenta sempre il numero di deceduti: contrariamente al grafico di prima, ogni singolo punto indica qui il numero di morti totale, a partire dal primo giorno (il 24 Febbraio), non quelli giornalieri.

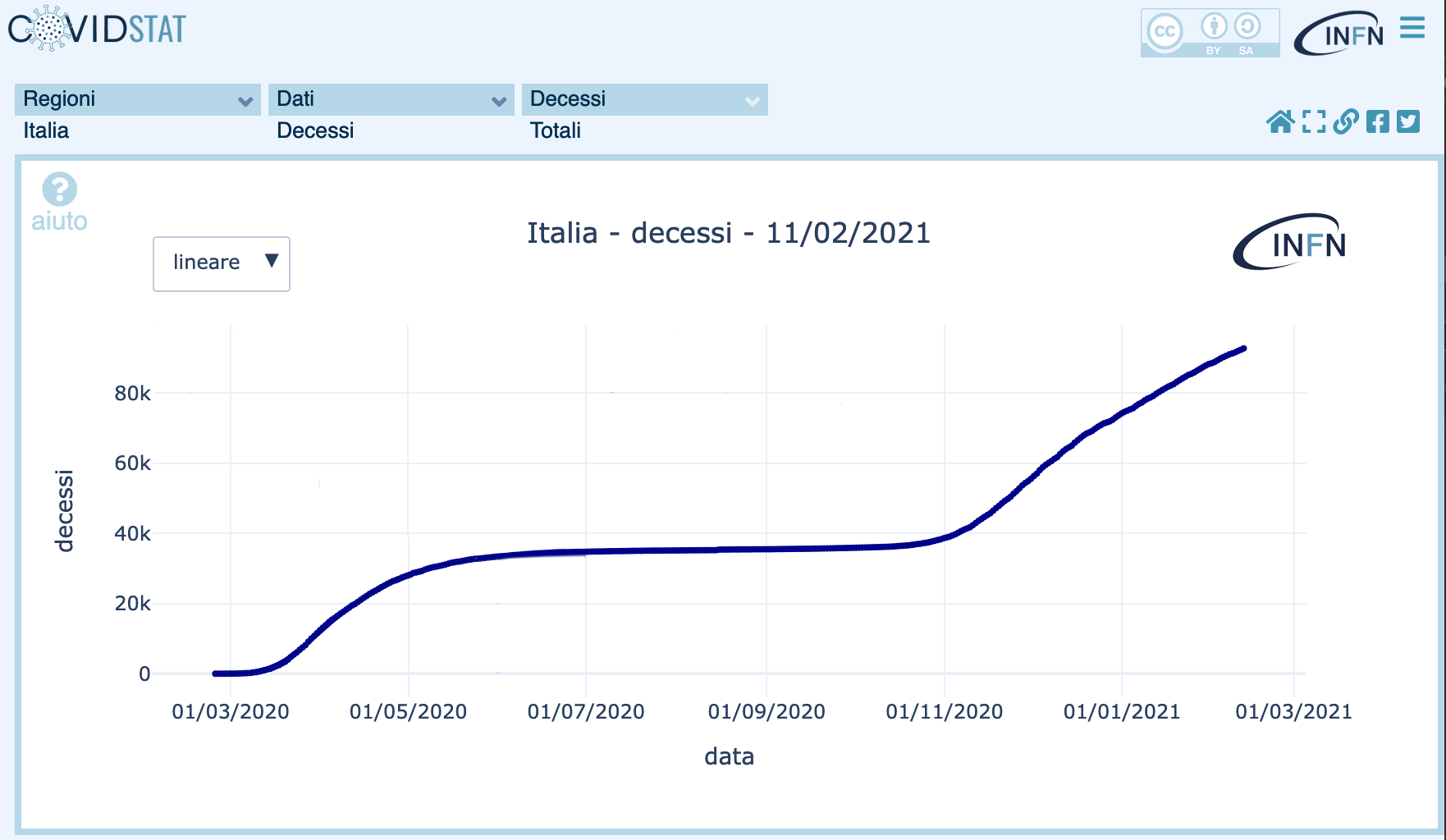Figura 3. Andamento totale dei decessi a partire dal 24 Febbraio 2020

In questo modo ogni punto contiene in sè tutti i valori dei punti precedenti: è quindi evidente che la curva non può che salire sempre. Se a partire da un certo giorno non ci sono più nuovi casi di morte, da quel momento in avanti la curva resta, al meglio, piatta, perchè non ci sono nuovi casi da sommare ai giorni precedenti. Non potrà mai scendere quindi a meno che qualcuno possa uscire dalla categoria dei deceduti, andando in sottrazione al totale (ma questo è purtroppo impossibile).

La curva della figura 2 prende il nome di curva differenziale, perchè presenta in ogni giorno un valore nuovo rispetto al giorno precedente, mentra quella della figura 3 rappresenta una curva detta integrale perchè ogni punto è la somma del valore odierno con quelli di tutti i giorni precedenti (ogni punto integra in sè il valore di quello che lo precede).

La rappresentazione differenziale e quella integrale costituiscono una la trasformazione dell’altra. Che relazione c’è quindi tra le due?

Consideriamo la figura 4, in cui rappresentiamo entrambe le curve nello stesso grafico, per permettere un confronto diretto tra le due.

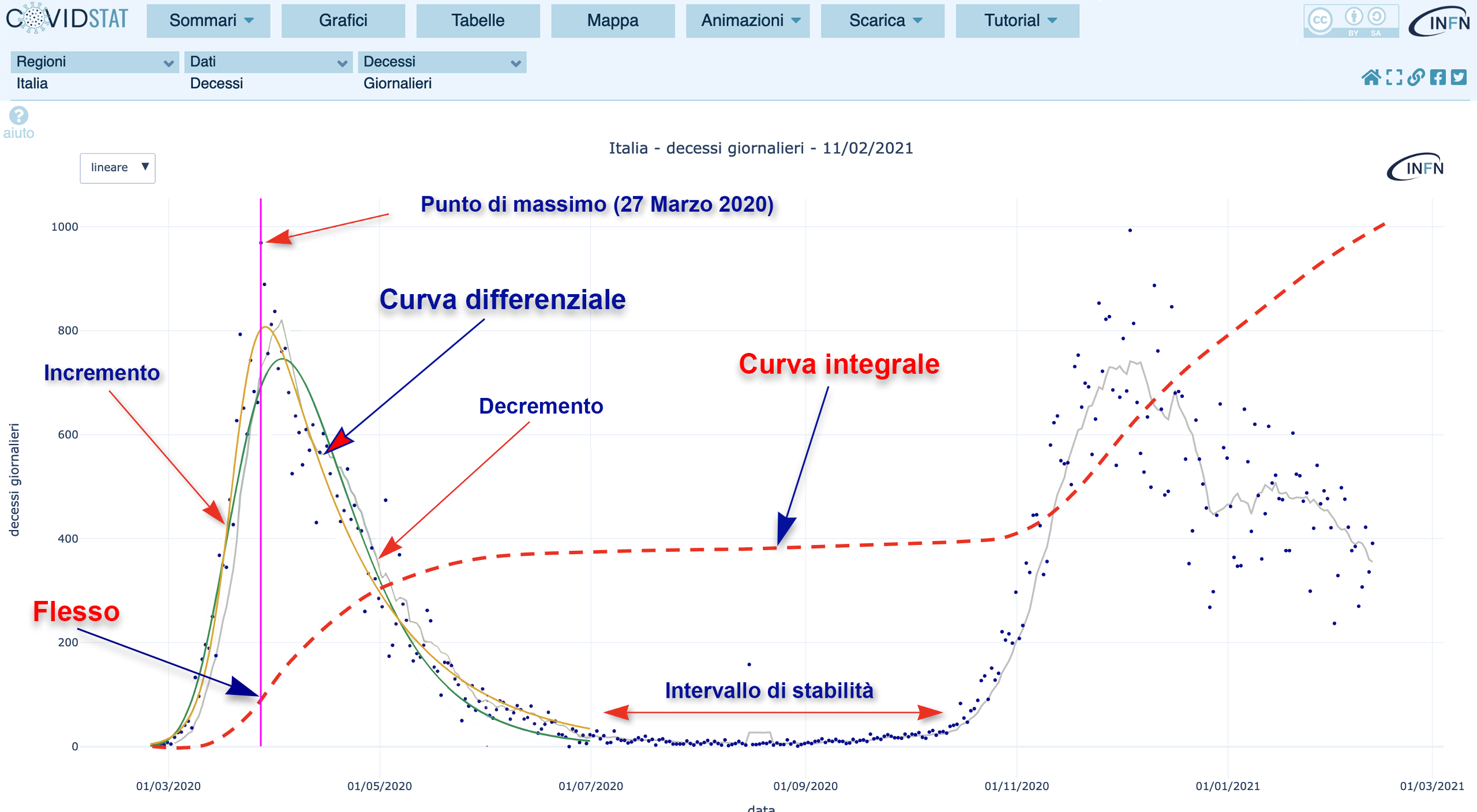Figura 4. Curva differenziale e curva integrale sovrapposte nello stesso grafico

Quando la curva differenziale (rappresentata dai punti blu) raggiunge un massimo, la curva integrale attraversa un “flesso“, un cambiamento di pendenza: quel che accade è che fino al quel momento (nel nostro caso il 27 Marzo 2020), ogni giorno ci sono stati più casi che nel giorno precedente. La curva differenziale è salita quindi rapidamente. Più casi nuovi ci sono ogni giorno, più rapidamente sale la curva. Per definizione, passato il massimo, ogni nuovo giorno ci sono meno casi che nel precedente e la curva inizia a scendere.

La curva integrale reagisce a questo stato di cose cambiando pendenza in corrispondenza del giorno in cui si raggiunge il massimo (il punto di flesso). Questo perchè ogni giorno la curva integrale assomma a sè valori sempre crescenti, ma quando si raggiunge il massimo i valori che si accumulano lo fanno con meno rapidità e quindi la curva integrale tende ad ammorbidire il suo tasso di crescita. Esaminiano questo punto con due esempi semplici, come quelli in figura 5.

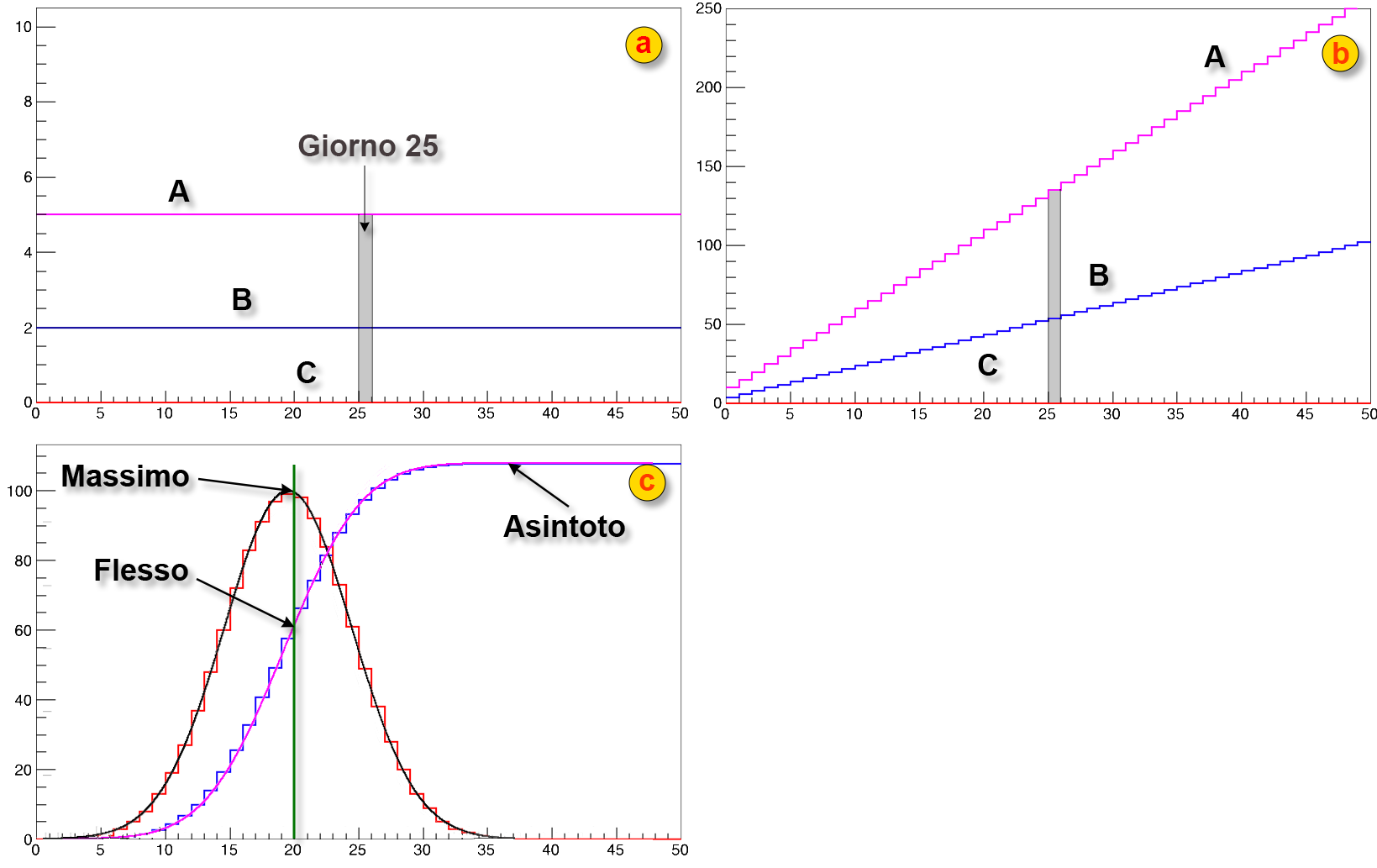Figura 5. Un esempio semplificato di curve differenziali e integrali, come descritto nel testo.

Nella prima in altro a sinistra, a,  abbiamo un grafico il cui asse orizzontale rappresenta 50 giorni: il primo giorno inizia a zero e dura fino alla prima stanghetta verticale. Il giorno 25, indicato in grigio, va da 25 a 26 e così via per tutti gli altri. L’asse verticale, invece, rappresenta il numero di volte in cui una persona mette dei soldi nel salvadanaio. Abbiamo i casi di tre diversi ragazzi, Anna, Bruno e Carlo. Carlo, il meno risparmioso, non mette mai un Euro da parte, ogni giorno che passa il suo salvadanaio segna zero (la linea rossa orizzontale). Il suo amico Bruno invece riesce a metterci ogni giorno 2 Euro, senza mai mancarne un giorno (la riga blu, attestata al valore 2). Infine, Anna, la più saggia, ce ne mette 5 ogni volta (la riga viola). Si vede subito che tutti e tre sono molto “costanti” nelle loro azioni, infatti le curve che rappresentano i soldi versati sono costanti, per un ammontare sempre uguale e mostrano quindi una pendenza nulla. Queste tre sono esempi di curve differenziali, rappresentano il contributo quotidiano, parcellizzato nel tempo.

Vediamo ora il grafico a destra, b. Si tratta sempre di Carlo, Bruno, e Anna e dei loro risparmi, ma questa volta rappresentano, giorno per giorno, quanto c’è in totale nei loro salvadanai. Per Carlo, come ci aspettiamo non avendoci mai messo un Euro, ogni giorno che passa il suo ammontare resta zero (la curva rossa). Per Bruno la situazione migliora ogni giorno: il primo giorno ci sono 2 Euro, il secondo sono 4, il terzo arriva a 6 e così via. Già qui si osserva un fatto interessante. Sia i versamenti di Carlo che quelli di Bruno sono costanti, ammontano, individualmente, alla stessa quantità giornaliera (diversa per i due ragazzi) e quindi sono rappresentati entrambi da una retta orizzontale nel grafico a. Se verifichiamo invece il totale dei loro risparmi accumulati, nel grafico b, mentre la retta di Carlo resta orizzontale, quella di Bruno è inclinata di un certo angolo. Veniamo ora ad Anna: i suoi risparmi crescono più velocemente di quelli di Bruno e certamente molto di più di quelli di Carlo: la retta che rappresenta i suoi risparmi (A) è quindi molto più inclinata di quella di Carlo e di Bruno (C e B).

Il grafico a rappresenta le curve differenziali dei loro versamenti (le chiamo “curve” in generale, anche se in questo esempio sono delle “rette“), mentre il grafico b rappresenta le curve integrali. In a quel viene evidenziato è il contributo quotidiano ai versamenti (0, 2 o 6 Euro), corrispondente al valore sull’asse verticale al quale si attestano le tre curve ogni giorno. In b conta, invece, la pendenza della curva. Poichè Anna versa 3 Euro in più al giorno rispetto a Bruno, i suoi risparmi crescono più velocemente: la pendenza della curva è l’indice di quanto più velocemente crescono. Il passaggio dalle curve a a quelle b si chiama integrale, mentre il passaggio inverso si chiama derivata. Prendiamo la curva A in b: se consideriamo il risparmio totale raggiunto nel giorno 25 e lo confrontiamo con quello del giorno precedente facendo la differenza, otteniamo 125-120=5, proprio quanto versato quel giorno (infatti 5 Euro al giorno per 25 giorni uguale 125).

Quando la curva differenziale si appiattisce significa che ogni nuovo giorno ci sono gli stessi valori del giorno precedente: se questi valori sono molti pochi si accumulano come una fievole nevicata e la pendenza della curva integrale resta quasi orizzontale. Diventa esattemente orizzontale solo se non ci sono in quei giorni dei nuovi contributi, per cui ogni giorno la situazione resta identica a quelli precedenti. Mentre un andamento piatto nella curva differenziale implica quindi una situazione stabile, questo si trasforma in una pendenza costante ma non nulla in quella integrale.

Passiamo ora al riquadro c della figura 5. Qui abbiamo una curva a campana (in rosso) che rappresenta i versamenti quotidiani di un loro amcio, Giorgio. Giorgio ha trovato un impiego e decide saggiamente di mettere da parte un bel gruzzoletto. Inizia il quarto giorno dopo essere stato assunto con un paio di Euro. Ma già il giorno dopo aumenta il suo versamento. Continua a farlo (ad aumentare l’importo quotidiano) fino al giorno 12: quel giorno sente dire in ufficio che dovrà lavorare da casa per qualche giorno alla settimana (causa COVID). Incerto su cosa si prospetti, decide di diminuire la cifra quotidiana da mettere nel salvadanaio: la curva rossa, che stava crescendo sempre più velocemente, adesso lo fa ancora, ma più lentamente. Il giorno 20 gli comunicano che, spiacenti, ma sono costretti a diminuirgli lo stipendio. In difficoltà con le spese quotidiane, Giorgio non solo non può più mettere da parte soldi, ma è costretto a diminuire drasticamente i risparmi. La curva dei versamenti quindi il 20 si inverte, non cresce più e inizia a diminuire. Il giorno 36, perso il lavoro, Giorgio non può più mettere da parte nulla e la curva, differenziale, diventa come quella di Carlo, piatta e a zero.

Vediamo ora la corrispondente curva integrale, rappresentata dalla linea blu in c. Come nel caso precedente si tratta di graficare il totale accumulato nel salvadanio nel tempo (Giorgio non ha mai prelevato soldi in quel periodo: se lo avesse fatto la curva rossa presenterebbe dei valori negativi, sotto lo zero). Fintanto che Giorgio ha immesso soldi, il totale cresceva sempre più velocemente: raggiunto il massimo della curva rossa, il valore accumulato nel salvadanaio raggiunge a sua volta il massimo della velocità di aumento, nella curva blu. Questo è testimoniato dal fatto che la curva blu, a quel punto, il giorno 20, cambia pendenza (un punto di flesso) e prosegue aumentando meno velocemente. Approssimandosi al giorno 36, i magri aumenti quotidiani di Giorgio volgono purtroppo a zero. Da quel giorno il contenuto del salvadanaio non aumenta più, si raggiunge un valore orizzontale costante. Il valore, sull’asse verticale , che viene raggiunto dalla curva blu rappresenta l’area della curva differenziale rossa (il totale della cifra risparmiata).
Qui ho riscalato verticalmente la curva blu per poterla sovrapporre a quella rossa: bisogna tener conto che la curva blu cresce sull’asse verticale molto più rapidamente che non la curva rossa.

Tutte le curve mostrate in figura 5 prendono il nome generico di “distribuzioni“. Una curva a campana come quella rossa emerge come fatto molto comune in una vastissima classe di fenomeni: la distribuzione delle altezze degli individui di una nazione è in genere descritta da una curva di quel genere, così come il reddito pro-capite, il numero di animali che fanno parte di un branco e innumerevoli altri fenomeni.

Di interesse per noi, in questo blog, sono i casi di infezione da COVID: ci aspettiamo che un’epidemia inizi da zero casi, aumenti con una qualche rapidità nel tempo, raggiunga un massimo e poi, sperabilmente, tenda a spegnersi. In genere epidemie come l’influenza hanno proprio questo comportamento. A seconda della virulenza e delle condizioni climatiche possono variare sia il giorno dell’anno in cui iniziano a manifestarsi, la velocità con cui si diffonde (la pendenza della curva differenziale) che il giorno di raggiungimento del massimo. Se poi vengono intraprese azioni specifiche, quali un lock-down, per alterare la capacità di diffusione dell’epidemia, si avrà come risultato un’alterazione della forma a campana localizzata nel tempo al momento in cui questa viene attuata, con un ritardo dovuto al tempo necessario tra incubazione della malattia e il suo manifestarsi in un decesso.

Tutti questi aspetti possono essere valutati sia dalla curva integrale che da quella differenziale. Vedremo in un prossimo blog come valutare quale sia la curva più appropriata nei diversi casi.