Guardando i grafici del nostro sito avrete notato che ognuno di essi possiede un menu a tendina che dice “Lineare” piuttosto che non “Log”. Molti avranno provato a selezionare “Log” e avranno notato che la forma delle curve si modifica in seguito a questa azione. Chiediamoci quale utilità presenti questa opzione. Di fatto ci permette di essere messi sull’avviso dell’instaurarsi di una condizione di variazione dell’entità di un fenomeno in modo più efficiente che non usando la scala lineare. Vediamo un esempio di quanto affermiamo in figura 1.
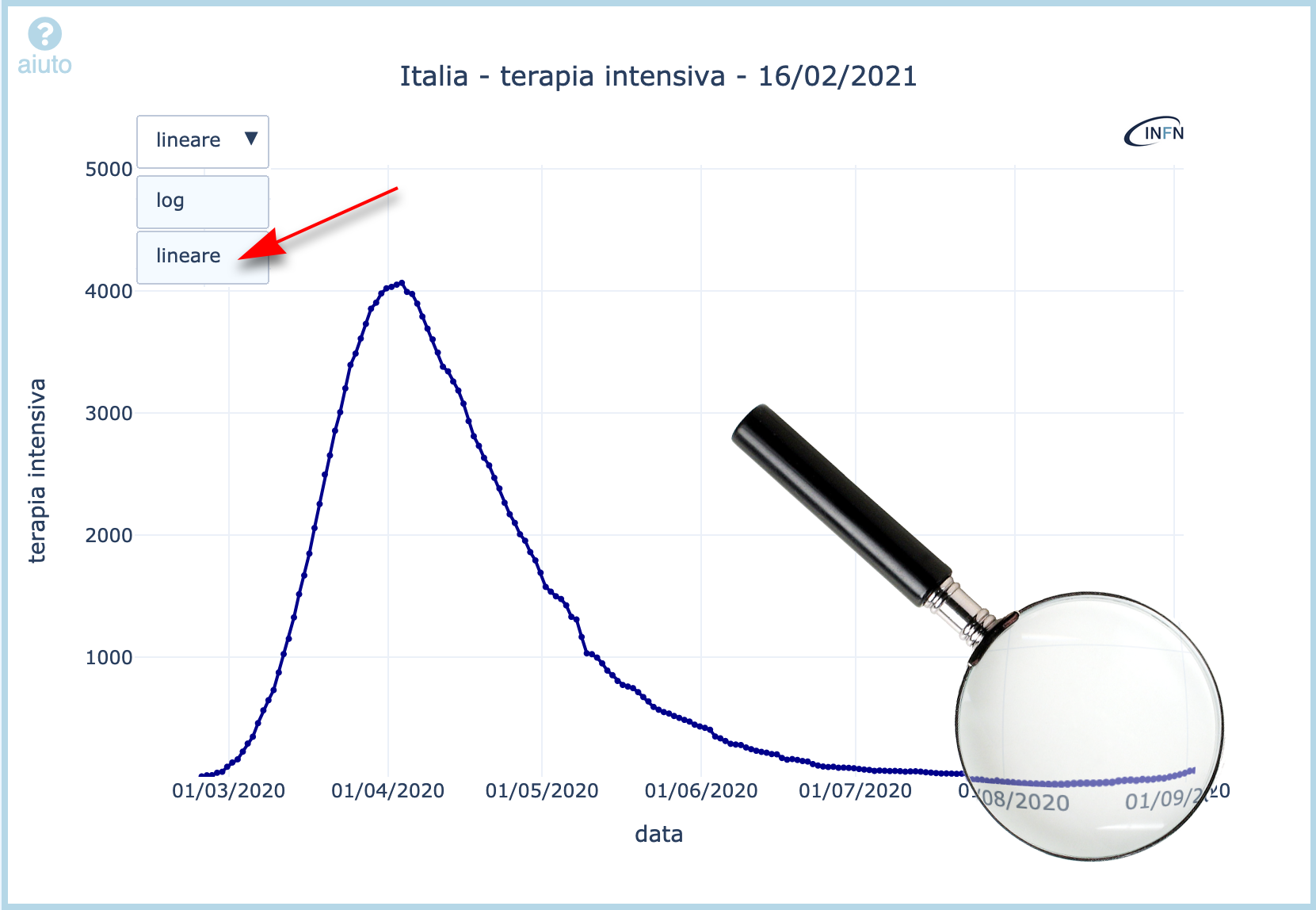 Figura 1: andamento temporale del numero di ricoverati in terapia intensiva dal 24 Febbraio al 1 Settembre 2020.
Figura 1: andamento temporale del numero di ricoverati in terapia intensiva dal 24 Febbraio al 1 Settembre 2020.
Molti, vedendo questo grafico verso la fine di Agosto, avranno commentato felici che la pandemia si era evidentemente spenta. Il numero di ricoverati in terapia intensiva si era infatti ridotto dal terribile valore di 4068 ricoverati al 3 Aprile a soli 43 al 1 Agosto e, apparentemente, come si vede in figura, non si erano discostati in modo evidente da quel piccolo valore.
Grave errore!
Se infatti selezioniamo la vista in scala logaritmica, come illustrato in figura 2, ci salta subito all’occhio un fatto che in scala lineare rimaneva, diciamo così, nascosto.
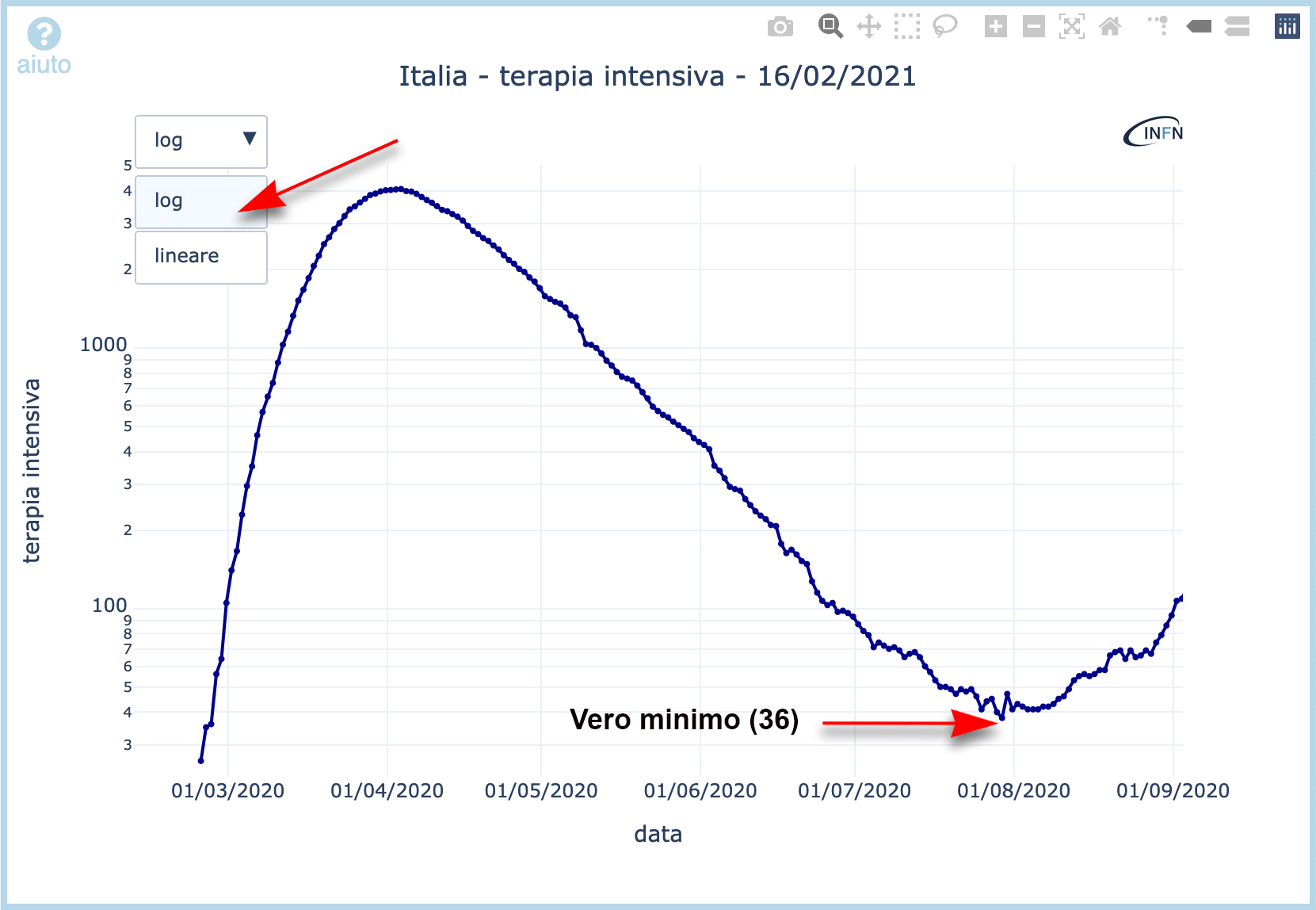
Figura 2. Stessi dati della figura 1, ma rappresentati con una scala logaritmica
In effetti il 1 Agosto il numero di ricoverati raggingeva un minimo, cosa che viene confermata anche da questa rappresentazione. Ma guardando con attenzione si vede che il vero minimo era già stato raggiunto il 29 Luglio, tre giorni prima, cosa che in scala lineare risulta difficile discernere. Ma la cosa eclatante che emerge dalla figura 2 è che a partire dal 5 Agosto il numero di ricoverati aveva ripreso a crescere dal valore di 41 fino a 107 ricoverati il 1 Settembre. In meno di un mese i casi erano più che raddoppiati!
E, cosa importante, questo fatto non si scorgeva guardando il grafico in figura 1.
I due grafici, lo ripetiamo per chiarezza, contengono gli stessi identici dati, sono solo rappresentati graficamente in due modi diversi. Detto in altri termini, se uno legge direttamente i numeri, senza passare dalla rappresentazione grafica, sempre quelli sono (e quindi uno ha modo così di accorgersi dell’incremento, se fa particolare attenzione). Grazie alla scala logaritmica, vengono amplificate verticalmente le variazioni di valori.
In questi dati c’è una grande disparità tra il numero di casi del primo picco (intorno al 3 Aprile, con 4068 ricoverati) e quello dei primi di Agosto (~40) e questo si traduce nel fatto che la variazione in questo mese rimane depressa nel confronto con Aprile, non si nota perchè risptto alla scala verticale globale consta di un numero piccolo. Era quindi facilissimo convincersi, con uno sguardo superficiale ai dati, che la pandemia si stesse ormai spegnendo. A onor del vero il biologo Enrico Bucci aveva messo sull’avviso i suoi lettori, ma venne tacitato dai colleghi con l’affermazione che la scala logaritmica fosse una sorta di banale lente di ingrandimento e quindi si volesse offrire un’immagine “distorta” della realtà (!). Ricordiamo tutti le affermazioni circa il fatto che il virus fosse ormai clinicamente morto (posto che un virus, non essendo un essere vivente, possa in effetti morire).
Ecco dove la matematica ci viene invece in aiuto (ma serve conoscerla, altrimenti si prendono lucciole per lanterne): cos’è una scala logaritmica?
Si tratta di un’operazione di deformazione della scala verticale. Mentre in un normale grafico ogni tacca dell’asse verticale corrisponde ad uno stesso incremento (la tacca a 50 dista da quella a 60 esattamente della stessa quantità che esiste tra la tacca a 1050 e a 1060), la rappresentazione logaritmica di un asse accorcia sempre più la distanza tra le tacche mano a mano che si aumenta di valori. Detto in altre parole, la distanza grafica tra 10 e 100 è uguale alla distanza tra 100 e 1000, pur essendoci uno scarto numerico di 89 unità nel primo caso e di 899 nel secondo.
Qual’è l’effetto (e lo scopo) di questa deformazione?
È proprio quello di amplificare la variazione di pendenza di una curva: il tratto che va dal primo Agosto al primo Settembre appare, in scala lineare, trascurabile rispetto alla grande salita e discesa del picco della prima ondata. Se osservato in scala logaritmica, invece, la pendenza della variazione viene amplificata e si nota a occhio.
Non si tratta di un bieco trucco, i valori numerici NON vengono cambiati dalla deformazione, quel che viene reso evidente è che la variazione non pare più piatta (quindi con nessun aumento di casi apparente) ma presenta invece un marcato valore.
Vediamo un altro caso in cui la deformazione introdotta dalla scala logaritmica ci permette di evidenziare un andamento che nei dati c’è ma che la scala lineare fa apparire trascurabile. In figura 3 vediamo l’andamento di diverse categorie di casi in Lombardia tra il 24 Febbraio 2020 e il 16 Febbraio 2021 (quasi un anno di pandemia).
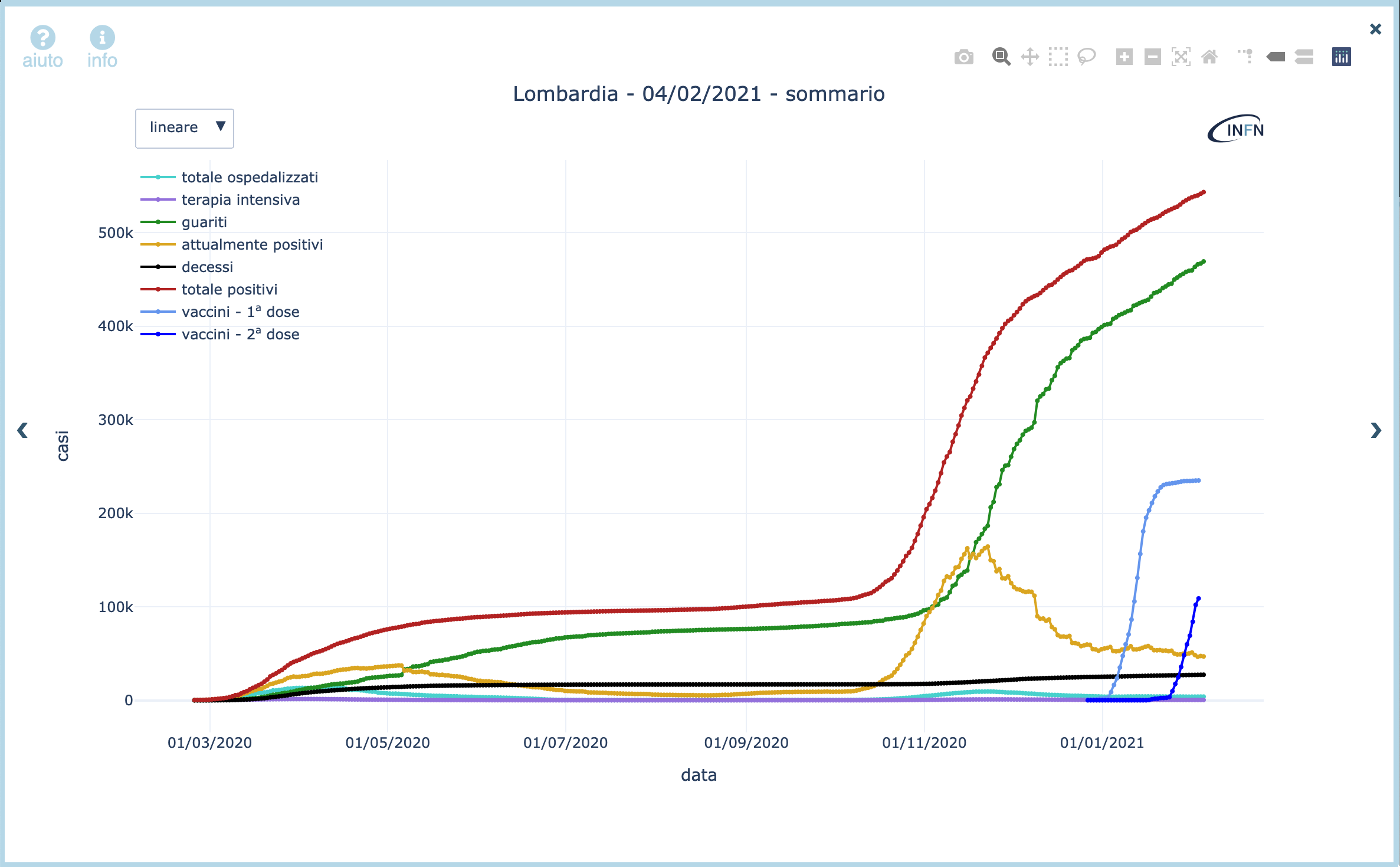 Figura 3: andamento di diverse categorie per la regione Lombardia tra il 24 Febbraio 2020 e 16 Febbraio 2021.
Figura 3: andamento di diverse categorie per la regione Lombardia tra il 24 Febbraio 2020 e 16 Febbraio 2021.
La curva più appariscente è la rossa, che corrisponde al numero totale di positivi a una certa data (una curva di tipo integrale, come sappiamo, vedi questo blog precedente). Le curve che descrivono l’andamento degli attualmente positivi (quelli che lo sono alla data specificata sull’asse orizzontale è una curva di tipo differenziale perchè i suoi valori possono sia crescere che diminuire nel tempo), quello degli ospedalizzati e quello dei ricoverati nelle terapie intensive (anch’esse curve di tipo differenziale) paiono trascuarbili al confronto ma, soprattutto, paiono privi di qualsiasi stuttura di crescita o diminuzione. Parrebbero indicare una situazione tranquilla ed accettabile.
Vediamo però gli stessi dati rappresentati in scala logaritmica, come illustrato in figura 4.
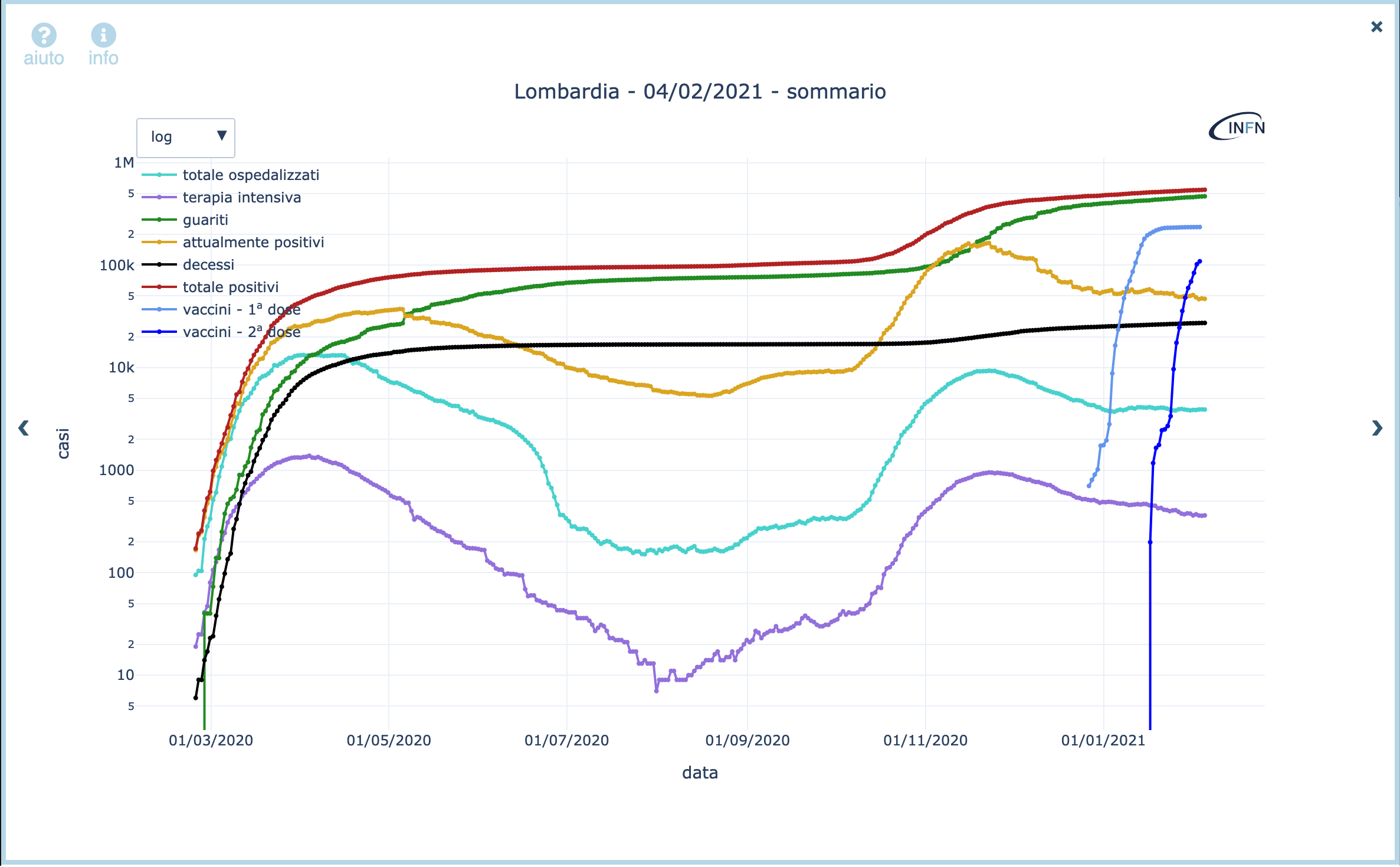 Figura 4: stessi dati della figura 3, ma espressi con una scala verticale logaritmica.
Figura 4: stessi dati della figura 3, ma espressi con una scala verticale logaritmica.
Ecco che le tre curve differenziali appena menzionate non appaiono più per nulla “piatte“, ma mostrano una marcata variazione. Raggiunto il primo picco in Aprile, tutte e tre le curve iniziano una lenta discesa, raggiungono un minimo in estate e riprendono a salire in autunno, raggiungendo il picco della seconda ondata. Si vede inoltre che, a partire da Aprile, il numero di attualmente positivi è in media circa dieci volte maggiore del numero di ospedalizzati che, a sua volta, è dieci volte maggiore dei ricoverati in terapia intensiva rapporti che si mantengono per tutto l’anno, fatti, questi, che in scala lineare non si notavano per nulla.
La matematica non è quindi nè inutile nè una lente deformante: ci permette, anche senza fare alcun conto, di visualizzare, di evidenziare correttamente dei fenomeni che in una particolare rappresentazione non appaiono mentre lo anno in un’altra opportunamente scelta. Questa constatazione (ovvia) è di enorme importanza, in particolarein un paese che da sempre predilige la sola cultura umanistica come “vera” cultura, relegando quella scientifica a mera technè (τέχνη).
Il passaggio da rappresentazione lineare a logaritmica non è l’unica deformazione possibile che si può applicare ai dati. Già nel 1569 il cartografo fiammingo Gerardo Mercatore aveva trovato un’utile rappresentazione geometrica della superficie terrestre che gli permetteva di trasporre su una mappa piana la geografia del nostro pianeta. Sappiamo bene quanto sia difficile avvolgere un foglio attorno a un pallone senza piegare in alcun modo la carta in fastidiose pieghe. Quest’operazione è più facile se prendiamo un foglio di gomma deformabile e lo avvolgiamo sulla sfera come una calza aderente. Lo si può fare agevolmente a costo però di stiracchiarlo: se poi ricalcassimo i luoghi della superficie terrestre su questo foglio e lo riportassimo infine alla forma originale, piatta, i luoghi man mano più vicini ai poli risulterebbero fortemente deformati. Questa deformazione diventa evidente in figura 5.
 Figura 5: proiezione Mercatore di una mappa quadrettata su una sfera. Si nota le deformazione progressiva dei quadrati mano a mano che ci si avvicina ai polo: mentre gli archi AD, CB, EH e GF sono lunghi uguali, gli archi lungo i paralleli AB, DC, EF e GH si accorciano sino a diventare un singolo punto al polo.
Figura 5: proiezione Mercatore di una mappa quadrettata su una sfera. Si nota le deformazione progressiva dei quadrati mano a mano che ci si avvicina ai polo: mentre gli archi AD, CB, EH e GF sono lunghi uguali, gli archi lungo i paralleli AB, DC, EF e GH si accorciano sino a diventare un singolo punto al polo.
la Groenlandia, sulle mappe a proiezione di Mercatore, appare in effetti molto più grande di quanto non sia in realtà, a causa della deformazione. Ma allora perchè distorcere i dati?
Semplice: la mappa distorta gode di un’utilissima proprietà: mantiene costanti gli angoli tra tre punti qualsiasi, permettendo quindi, a chi consultasse la mappa distorta, di calcolare la propria posizione nel globo usando solo bussola e compasso. Nel 1500 non esistevano orologi sufficientemente precisi per determinare la longitudine e queste mappe facevano la differenza tra ricchezza e tragedia per i mercanti navali e vittoria disfatta per gli eserciti.
Le deformazioni matematiche esercitano quindi un funzione fondamentale nella nostra capacità di osservare il mondo, posto che si abbia contezza della sottostante matematica.
Semplice chiaro utile. Grazie.
Io uso una formula semplice per equilibrare tamponi e positivi.
La curva che risulta è ben differente da quelle che si vedono in giro.
Dove posso scaricare dati grezzi delle Province?
Grazie.
Grazie per il complimento.
I dati che utilizziamo sono quelli forniti dalla Protezione Civile: https://github.com/pcm-dpc/COVID-19/tree/master/dati-province
Un saluto